Week Four - Division

Synthesise the big ideas
The following are the big ideas that were discussed in week four:
- There are two types of division:
  1. Partition/sharing problems - "...a collection of objects is separated into a given number of
      equivalent groups and you need to determine the number in each group...Gary had 15 shells. If
      he wanted to share them equally among 5 friends, how many should he give to each" (Reys et
      al., 2012, p. 203).
  2. Measurement/repeated subtraction problems - "...you know how many objects are in each group
      but you must determine the number of groups...Jenny had 12 grapes. She gave 3 to each
      person. How many people received grapes?" (Reys et al., 2012, p. 203).
- There are four different thinking strategies for division:
  1. Use counting strategy for 5s and 10s
  2. Think real world for 1s and 0s
  3. Use doubles for 2s, 4s and 8s
  4. Build up or build down for 3s, 6s and 9s (Jamieson-Proctor, 2016).
- BEDMAS is the correct order in which mathematics operations should be performed (Smith, 2014)
  * B = brackets
  * E = exponents (i.e. squared, cubed)
  * D = division
  * M = multiplication
  * A = addition
  * S = subtraction
- Rules for division:
  * Even numbers can be divide by 2 without a remainder
  * Numbers that end in 5 or 0 can be divided by 5 evenly
  * Numbers ending in 0 can be divided by 10 evenly
  * By adding the digits of a number together you can tell if a number will be able to be divided by 3,
     if the total is a multiple of three than it will divide equally in to 3 with no remainders (Jamieson-
     Proctor, 2016).

My understanding of the weekly topic has changed in the following ways:
- My understanding of BEDMAS has changed after this week. This is because when I was in school
   I learnt BIMDAS and I didn't realise that it had changed.
- My understanding of division has also changed because I never knew how to find out if a number
  is able to be divided by 3 without doing the division.

Demonstrate your understanding of the mathematical concept and related skills and strategies children need to assimilate and be able to use, that are related to division
- The concept this week was division. Division is seperating a number in to equal parts (Jamieson-
   Proctor, 2016).
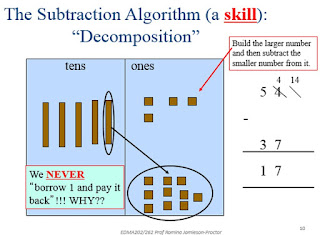
- The concept of division is applied using the skill of division algorithm. The division algorithm can
   be seen in figure 1.11 (Jamieson-Proctor, 2016).
- There are four different strategies for division:
   1. Use counting strategy for 5s and 10s
   2. Think real world for 1s and 0s
   3. Use doubles for 2s, 4s and 8s
   4. Build up or build down for 3s, 6s and 9s (Jamieson-Proctor, 2016).

Figure 1.12:  Jamieson-Proctor, R. (2016). EDMA202/262 Mathematics Learning and Teaching 1: Week 4 Part 2. Brisbane, Australia: Australian Catholic University. 

Language Model for Division

Figure 1.13: Language Model for Division

Describe/demonstrate a specific teaching strategy and appropriate resource/s that could be used to assist children to understand a key mathematical concept of division 
- A specific teaching strategy that could be used for children to understand the concept of division
  is the skip counting strategy. Skip counting is something that occurs in everyday life fro children
  and adults therefore it is an essential strategy to learn (Reys et al., 2012).
- An example of skip counting is 3, 6, 9, 12, 15, 18, 21, 24. This skip counting pattern is the a  
  sequence of the 3 times tables. An example of skip counting for division can be seen in the
  following video.
- When teaching skip counting a hundred chart would be helpful for students to visualise the normal
   number pattern and then figure out what the next number in their skip sequence would be. An
   example of a hundred chart can be seen in figure 1.10 in the week 3 blog.

Describe/demonstrate a specific misconception children might have in relation to division. How would you avoid or remediate this misconception?
- A common misconception about division is that division will always make a number smaller. When
  dividing rational numbers that are lower than one, this will not always be the case (Graeber &
  Campbell, 1993).
- It is important that children don't always believe that division makes numbers smaller as this will
  effect their mathematics skills in the later years of school.
- A way to remediate this would be to ensure that when teaching division children are never taught
  that division makes numbers smaller.

Provide appropriate URL links to the ACARA year, strand, substrand, content description, elaborations and Scootle resources for the earliest mention of division
- Division is first seen in the Australian Curriculum in Year 2 number and algebra strand, number
  and place value substrand.
- The content description for ACMNA032 is "recognise and represent division as grouping into equal
   sets and solve simple problems using these representations" (ACARA, 2016).
- The elaborations for ACMNA032 are "dividing the class or a collection of objects into equal-sized
  groups" and "identifying the difference between dividing a set of objects into three equal groups
  and dividing the same set of objects into groups of three" (ACARA, 2016).
- Scootle resources for division

Provide appropriate links to resources and ideas you have sourced personally to assist students to develop concepts, skills and/or strategies related to division
- Resource/s for students to understand the concept of division:
  * Concept of division
- Resources for students to understand the skill of division:
  * Short division
  * Long division
- Resources for students to understand the strategy of division:
  * Use counting strategy
  * Use doubles
  * For build up and build down the same videos that were used for multiplication can be used for
     division with teachers reiterating the relationship but difference between the two.

Provide a concise synthesis of the textbook chapter/s related to the weekly topic
- There are two types of division problems:
   * Measurement/repeated subtraction problems
   * Partition/sharing problems
- Thinking strategies for division - think multiplication and repeated subtraction
- Skills for division:
   * Division with 1 digit divisor
      e.g. 52 ÷ 7
             "52 divided by 7 is close to 49 divided by 7, which is 7. But there are 3 left over. So the
               answer is 7 remainder 3" (Reys et al., 2012, p. 263).
   *  Distributive algorithm
        e.g.

Figure 1.14: Reys, R., Lindquist, M., Lambdin, D., Smith, N., Rogers, A., Falle, J., Frid, S., & Bennett, S. (2012). Helping children learn mathematics. Queensland, Australia: John Wiley & Sons Australia, Ltd. 

   * Subtractive algorithm
      e.g.

Figure 1.15: Reys, R., Lindquist, M., Lambdin, D., Smith, N., Rogers, A., Falle, J., Frid, S., & Bennett, S. (2012). Helping children learn mathematics. Queensland, Australia: John Wiley & Sons Australia, Ltd. 

  * Division with 2 digit divisor - this type of division is mainly done with a calculator so teachers

     don't need to spend months with students developing this skill (Reys et al., 2012).

References

Australian Curriculum and Assessment, Reporting Authority [ACARA]. (2016). Mathematics. Retrieved from http://www.australiancurriculum.edu.au/mathematics/curriculum/f-10?layout=1

Education Services Australia. (2016). Scootle: Mathematics. Retrieved from http://www.scootle.edu.au/ec/search?accContentId=ACMNA032&userlevel=(2)

Graeber, A. & Campbell, P. (1993). Misconceptions about multiplication and division. The Arithmetic Teacher, 40(7), 408-411.  

Howard, C. (2015). EDX1280 use doubles strategy for multiplication and division. Retrieved from https://www.youtube.com/watch?v=xQdkzhYZQd0

Iken Edu. (2011). Division made easy: Math video to learn division basics. Retrieved from https://www.youtube.com/watch?v=wBSVDxqCTWw

Jamieson-Proctor, R. (2016a). EDMA202/262 Mathematics learning and teaching 1: Week 4 part 2. Brisbane, Australia: Australian Catholic University.

MathsMaster.Org. (2011). Short division. Retrieved from https://www.youtube.com/watch?v=oWyTxq5mewo

Mr Judy’s Class. (2013). Skip counting for division. Retrieved from https://www.youtube.com/watch?v=bOBKsnkUGx4

Reys, R., Lindquist, M., Lambdin, D., Smith, N., Rogers, A., Falle, J., Frid, S., & Bennett, S. (2012). Helping children learn mathematics. Queensland, Australia: John Wiley & Sons Australia, Ltd.

Smith. (2014). Maths quest 8 for Victoria: Australian curriculum edition. Retrieved from http://leo.acu.edu.au/pluginfile.php/1486742/mod_book/chapter/32719/BODMAS%20example.pdf

Tecmath. (2011). Long division: easy. Retrieved from https://www.youtube.com/watch?v=vzI3bqk2_fg

Week Three - Multiplication

Synthesise the big ideas
In week three the following big ideas were covered:
- There are four different ways to model multiplication (Jamieson-Proctor, 2016a):
  1. Set model - there are 2 acorns on each of the 3 plates. How many acorns are there all together?
  2. The array/area model - the length of a rectangle is 5 centimetres and the width is 3 centimetres.
      What is the area of the rectangle?
  3. The measurement/length model - I bought 4 hair ribbons each 2 metres long. How many metres
       of ribbon did I buy?
  4. The combinations/cross products model - I have 3 different coloured shirts and 2 different
      coloured pants. How many different outfits can I make?
- There are five different strategies for multiplication (Jamieson-Proctor, 2016a):
  1. Use counting strategy for x5 and x10
  2. Think real world for x1 and x0
  3. Use doubles for x2, x4 and x8
  4. Build up for x3, x5 and x6 or build down for x9 and x10
  5. The turn-around 7's
- There are five different properties for multiplication (Reys et al., 2012):
   1. Null factor property - when a number is multiplied by 0 the product will be 0
   2. Identity property - when a number is multiplied by 1 it stays the same
   3. Commutative property/turnarounds - 3 x 4 is the same as 4 x 3
   4. Associative property - 3 x (4 x 5) is the same as 3 x (4 x 5)
   5. Distributive property - 4 x 7 = ?
                                         = 4 x (5 + 2)
                                         = (4 x 5) +  (4 x 2)
                                         = 20 + 8
                                         = 28
- "A factor is a whole number that can be divided into another whole number to given a whole
    number quotient" (Jamieson-Proctor, 2016b, p. 8). i.e. 2 x 3 = 6, the quotient is 2 and 3
- "A multiple is the quantity achieved by multiplying 2 or more factors together" (Jamieson-Proctor,
    2016b, p. 8). i.e. 2 x 3 = 6, the multiple is 6.
- Prime factorisation - all composite numbers are the product of a prime numbers if the order is
  ignored (Reys et al., 2012) i.e. 12 is the product of 2 x 2 x 3.
- Lowest Common Multiple (LCM) - the smallest number that a given group of numbers will
  divide into exactly (Jamieson-Proctor, 2016b) i.e. 2, 3, 5. Pick the highest number in the group
  and list the multiples to find the LCM. e.g. 5, 10, 15, 20, 25, 30, 35. LCM of 2, 3 and 5 is 30
- Greatest Common Factor (GCF) - the largest number that will divide into a group of numbers
   evenly. i.e. 6, 12, 18. Pick the lowest number in the group and list the multiples. Find the number
   that the numbers all divide equally into. e.g. 6 = 1, 2, 3 and 6. GCF of 6, 12 and 18 is 6.  

These big ideas have changed my understanding of the weekly topic in the following ways:
- I now have an understanding that there are four different ways to model multiplication
- I also have a greater understanding of prime factorisation, lowest common multiples and greatest
  common factors, allowing me to better teach these to students. Although I always knew what
  these concepts were I struggled with understanding them. I now understand them more.
- I also didn't know that there were five different properties for multiplication, I only knew about
  null factor, identity property and commutative property.

Demonstrate your understanding of the mathematical concept and related skills and strategies children need to assimilate and be able to use, that are related to the concept of multiplication
- The concept this week was multiplication. Multiplication is repeated addition of equal groups
  or sets. This concept of addition also involves the concepts of five different multiplication
  properties:
  1. Null factor property
  2. Identity property
  3. Commutative property
  4. Associative property
  5. Distributive property.
- The concept of multiplication is applied using the skill of multiplication algorithms. A
  multiplication algorithm can be seen in figure 1.8.
- There are five different strategies for the concept of multiplication;
   1. Use counting strategy
   2. Think real world
   3. Use doubles
   4. Build up
   5. The turn-around

Figure 1.8:  Jamieson-Proctor, R. (2016a). EDMA202/262 Mathematics Learning and Teaching 1: Week 3 Part 2. Brisbane, Australia: Australian Catholic University. 

Language model for multiplication

Figure 1.9: Language Model for Multiplication

Describe/demonstrate a specific teaching strategy and appropriate resource/s that could be used to assist children to understand the mathematical concept of multiplication 
- A specific teaching strategy that could be used for children to understand the concept of
  multiplication is the skip counting strategy. Skip counting is something that occurs in everyday life
  for children and adults therefore it is an essential strategy to learn (Reys et al., 2012).
- An example of skip counting is 5, 10, 15, 20, 25, 30. These numbers are part of the 5 times
  tables.
- When teaching skip counting a hundred chart would be helpful for students to visualise the normal
  number pattern and then figure out what the next number in their skip sequence would be. An
  example of a hundred chart can be seen in figure 1.10.

Figure 1.10: Smart About Mathematics (2016). Gallery of 100 chart for math. Retrieved from http://www.smart.dynu.net/100-chart-for-math.html 

Describe/demonstrate a specific misconception children might have in relation to multiplication. How would you avoid or remediate this misconception?
- A common misconception that children might have in relation to multiplication is that
  multiplication always makes a number bigger. This is a misconception that can affect children's
  mathematics ability when they are learning to multiply with rational numbers less than one
  (Graeber & Campbell, 1993).
- This misconception can be avoided by ensuring that when teaching the basics of multiplication
  children are not told or taught that multiplication always makes numbers bigger, to avoid confusion
  in the later years.

Provide appropriate URL links to the ACARA year, strand, sub-strand, content description, elaborations and Scootle resources for the earliest mention of multiplication
- Multiplication can be first seen in Year 2 of the Australian Curriculum, number and algebra strand,
  and in the number and place value sub-strand.
- The content description for ACMNA031 is "recognise and represent multiplication as repeated
   addition, groups and arrays" (ACARA, 2016).
- The elaborations are "representing array problems with available materials and explaining
   reasoning" and visualising a group of objects as a unit and using this to calculate the number of
   objects in several identical groups" (ACARA, 2016).
- Scootle resources for multiplication

Provide appropriate links to resources and ideas you have sourced personally to assist students to develop concepts, skills and/or strategies related to multiplication
- Resource/s for children to learn the concept of multiplication
  *concept of multiplication
- Resource/s for children to learn the skill of multiplication
  * multiplication algorithm
- Resource/s for children to learn the strategies of multiplication
  * Skip counting strategy 
  * Use doubles strategy
  * Build up strategy
  * Build down strategy

Provide a concise synthesis of the textbook chapter/s related to the weekly topic
- There are four types of multiplication problems:
  1. Equal group problems;
  2. Comparison problems;
  3. Combination problems;
  4. Area and array problems (Reys et al., 2012)
- Different skills for multiplication:
  * Multiplication with 1 digit multipliers (Reys et al., 2012)
        14
      x  2
     ------
          8       2 x 4 = 8
     + 20       2 x 10 = 20
    -------
        28
  * Partial-products multiplication algorithm (Reys et al.., 2012)
        372
      x  28
      ------
          16      (8 x2)
        560      (8 x 70)
      2400      (8 x 300)
          40      (20 x 2)
      1400      (20 x 70)
      6000      (20 x 300)
    ----------
     10416
   * Lattice multiplication algorithm
     

Figure 1.11: Reys, R., Lindquist, M., Lambdin, D., Smith, N., Rogers, A., Falle, J., Frid, S., & Bennett, S. (2012). Helping children learn mathematics. Queensland, Australia: John Wiley & Sons Australia, Ltd. 

   * Multiplication by 10 and multiples of 10 - whenever a number is multiplied by 10 all of the digits
      move 1 place to the left i.e. 10 x 863 = 8630 (Reys et al., 2012).
    * Multiplication with zeros (Reys et al., 2012)
         306
       x    9
      --------
        2754

       9 x 306 = 9 x (300 + 6)
                    = (9 x 300) + (9 x 6)
                    = 2700 + 54
                    = 2754
   * Multiplication with 2 digit multipliers (Reys et al., 2012)
        54
     x 23
    --------
        12
      150
        80
    1000
    -------
    1242
   * Multiplication with large numbers - when multiplying with large numbers children should be
      encouraged to estimate before using the calculator (Reys et al., 2012).
- There are six different thinking strategies for multiplication facts:
  1. Commutativity;
  2. Skip counting;
  3. Repeated addition;
  4. Splitting the product into known parts;
  5. Patterns;
  6. Multiplying by 1 and 0 (Reys et al., 2012).

References 

Australian Curriculum and Assessment, Reporting Authority [ACARA]. (2016). Mathematics. Retrieved from http://www.australiancurriculum.edu.au/mathematics/curriculum/f-10?layout=1

Education Services Australia. (2016). Scootle: Mathematics. Retrieved from http://www.scootle.edu.au/ec/search?accContentId=ACMNA031&userlevel=(2)

Graeber, A. & Campbell, P. (1993). Misconceptions about multiplication and division. The Arithmetic Teacher, 40(7), 408-411.  

Jamieson-Proctor, R. (2016a). EDMA202/262 Mathematics learning and teaching 1: Week 3 part 2. Brisbane, Australia: Australian Catholic University. 

Jamieson-Proctor, R. (2016b). EDMA202/262 Mathematics learning and teaching 1: Week 3 part 3. Brisbane, Australia: Australian Catholic University. 

Kisi Kids Math TV. (2013). Learn the basics of multiplication: Math lesson for 2^nd graders. Retrieved from https://www.youtube.com/watch?v=uacFH2oLj9M

Math Antics. (2012). Maths Antics: Multi-digit multiplication pt 1. Retrieved from https://www.youtube.com/watch?v=FJ5qLWP3Fqo

Origio One. (2016). Teaching the build-up strategy for multiplication. Retrieved from https://www.youtube.com/watch?v=NPC1mMKOl5I

Price, S. (2014). Build-down strategy folder card. Retrieved from https://www.youtube.com/watch?v=_sYUMQ4j5qY

Reys, R., Lindquist, M., Lambdin, D., Smith, N., Rogers, A., Falle, J., Frid, S., & Bennett, S. (2012). Helping children learn mathematics. Queensland, Australia: John Wiley & Sons Australia, Ltd.

Smart About Mathematics (2016). Gallery of 100 chart for math. Retrieved from http://www.smart.dynu.net/100-chart-for-math.html 

Tenframe. (2011). Times tables: Multiply with 4, use the doubles strategy. Retrieved from https://www.youtube.com/watch?v=Vnv4-MMOlas

Tenframe. (2011). Times tables: Multiply with 5, skip counting strategy. Retrieved from https://www.youtube.com/watch?v=R_Y8setGf5k

Week Two - Subtraction

Synthesise the big ideas
In week two the following big ideas were covered:
- That mathematics is what teachers teach and students develop numeracy (Jamieson-Proctor,
   2016).
- There are three different types of subtraction:
   1. Take-away - i.e. "I had 5 lollies and I ate 2. How many do I have left?".
   2. Difference/Comparison - i.e. "I have 5 lollies and you have 10 lollies. How many more do you
      have than me?" or "How many less do I have than you".
   3. Missing addend - i.e. "I have 3 lollies but I need 7 for all my friend. How many more lollies do
       I need?" (Jamieson-Proctor, 2016).
- There are three different strategies for subtraction:
  1. Count back,
  2. Use halves,
  3. Use tens (Jamieson-Proctor, 2016).
- Storybooks are a great way to teach subtraction.
- At a primary school level teachers need to consider that children's ability to learn mathematics can
  depend on their reading ability (Reys, Lindquist, Lambdin, Smith, Rogers, Falle, Frid & Bennett,
  2012).
- Students learn mathematics with understanding by actively building new knowledge from their
  personal experiences and prior knowledge (Reys et al., 2012).

These big ideas have changed my understanding on the weekly topic in the following ? ways;
1. I now have a greater understanding of subtraction after this week. Prior to this week I didn't
    realise that there was more than one type of subtraction.
2. This week has also given me a greater understanding of different strategies for teaching children
    subtraction

Demonstrate your understanding of the mathematical concept and related skills and strategies children need to assimilate and be able to use, that are related to subtraction
- The mathematical concept this week was subtraction. Subtraction is where the overall
  total and one part of the sum is known and you need to find the missing part.
- The concept of subtraction is applied using the skill of subtraction algorithm. This can be seen in
  figure 1.6.
- There are three strategies for the concept of subtraction; count back, use halves and use tens.

Figure 1.6:  Jamieson-Proctor, R. (2016). EDMA202/262 Mathematics Learning and Teaching 1: Week 2 Part 2. Brisbane, Australia: Australian Catholic University. 

Language Model for Subtraction

Figure 1.7: Language Model for Subtraction

Describe/demonstrate a specific teaching strategy and appropriate resource/s that could be used to assist children to understand the mathematical concept of subtraction 
- A specific teaching strategy that could be used for children to understand the concept of
  subtraction is the count on strategy. Children struggle to count backwards and therefore there
  should be learning experiences available for children to learn to count backwards (Reys et al.,
  2012). Children would be encouraged to count back from the highest number.
- An example of the count back strategy would be "Max had 12 eggs and broke 4 eggs. How many
  eggs does Max have left?" 12, 11, 10, 9, 8.
- When practising subtraction in the children and materials language stage I would use resources,
   such as pictures, toys, MAB blocks, counters and other concrete materials. By using these
   concrete materials students are able to physically count on to reach their final answer. An
   example of how this would work can be seen in the Matholia Channel video.

Describe/demonstrate a specific misconception children might have in relation to subtraction. How would you avoid or remediate this misconception?
- A common misconception for subtraction is that it is only 'take away', when in fact there are
  three kinds of subtraction. A way to remediate this misconception is to make sure that the proper
  subtraction language is used, such as 'subtract' or 'minus', instead of 'take away' to avoid
  confusion (Harris, 2000).

Provide appropriate URL links to the ACARA year, strand, substrand, content description, elaborations and Scootle resources for the earliest mention of subtraction 
- Subtraction can first be seen in Year One of the Australian Curriculum, in the number and algebra
  strand, and the number and place value sub-strand.
- The content description for ACMNA015 is "represent and solve simple addition and subtraction
  problems using a range of strategies including counting on, partitioning and rearranging parts"
  (ACARA, 2016).
- The elaboration is "developing a range of mental strategies for addition and subtraction problems"
  (ACARA, 2016).
- Scootle resources for subtraction

Provide appropriate links to resources and ideas you have sourced personally to assist students to develop concepts, skills and/or strategies related to subtraction
- Resource/s for students to understand the concept of subtraction
  * subtraction song
- Resource/s for students to understand the skill of subtraction
  * subtraction algorithm 
- Resource/s for students to understand the strategies of subtraction
  * counting back strategy
  * use tens strategy
  * use doubles strategy

Provide a concise synthesis of the textbook chapter/s related to the weekly topic
- Teachers can support the diverse learners in the classroom by:
   * Creating a positive learning environment;
   * Avoiding negative experiences that increase anxiety;
   * Establishing clear expectations;
   * Treating all students as equally likely to have aptitude for mathematics;
   * Helping students improve their ability to retain mathematical knowledge and skills (Reys et al.,
     2012).
- At a primary school level teachers need to consider that the children's ability to learn mathematics
  can depend on their reading ability (Reys et al., 2012).
- There are three types of subtraction:
   1. Separation problems - "...involves having one quantity, removing a specified quantity from it
       and noting what is left" (Reys et al., 2012, p. 200). i.e. "Wan had 7 balloons. She gave 4 to
       other children. How many did she have left?" (Reys et al., 2012, p. 200).
   2. Comparison problems - "...involves having 2 quantities, matching them 1 to 1 and noting the
       quantity that is the difference between them" (Reys et al., 2012, p. 200). i.e. "Wan had 7
       balloons. Richard had 4 balloons. How many more balloons did Wan have than Richard?"
       (Reys et al., 2012, p. 200).
   3. Part-whole problems - "...a set of objects can logically be separated into 2 parts. You know
       how many are in the entire set and you know how many are in one of the parts. You need to
       find out how many must be in the remaining part" (Reys et al., 2012, p. 200). "Wan had
       7 balloons. Four of the were red and the rest were blue. How many were blue?" (Reys et al.,
       p. 200).
- There are two different skills for subtraction:
  * Standard subtraction algorithm
          91               11 - 4 = 7 ones
        - 24                8 tens - 2 tens = 6 tens
       -------
          67
  * Partial-difference subtraction algorithm
           523
        - 385
      -----------
          200
        -  60
        -    2
      -----------
          140
        -    2
      ----------
          138
- There are four thinking strategies for subtraction facts:
  1. Subtracting 1 and 2
  2. Doubles
  3. Counting back
  4. Counting on (Reys et al., 2012).

References 

Australian Curriculum and Assessment, Reporting Authority [ACARA]. (2016). Mathematics. Retrieved from http://www.australiancurriculum.edu.au/mathematics/curriculum/f-10?layout=1

Beams, H. (2013). Subtraction with the make ten strategy. Retrieved from https://www.youtube.com/watch?v=n3fY7DbyEUo

Education Services Australia. (2016). Scootle: Mathematics. Retrieved from http://www.scootle.edu.au/ec/search?accContentId=ACMNA015&userlevel=(1)

Gray, S. (2011). Using doubles and building on doubles: A mental math subtraction strategy. Retrieved from https://www.youtube.com/watch?v=E9_oZ3ew56I

Harris, A. (2000). Addition and subtraction. Retrieved from http://ictedusrv.cumbria.ac.uk/maths/pgdl/unit5/A&S.pdf 

Harry Kindergarten Music. (2014). When you subtract with a pirate. Retrieved from https://www.youtube.com/watch?v=QkPa9V2wtZs

Jamieson-Proctor, R. (2016). EDMA202/262 Mathematics learning and teaching 1: Week 2 part 2. Brisbane, Australia: Australian Catholic University.

Mathantics. (2012). Math Antics: Multi-digit subtraction. Retrieved from https://www.youtube.com/watch?v=Y6M89-6106I

Matholia Channel. (2013). Subtract by counting back. Retrieved from https://www.youtube.com/watch?v=QhR1SEK49qM

Reys, R., Lindquist, M., Lambdin, D., Smith, N., Rogers, A., Falle, J., Frid, S., & Bennett, S. (2012). Helping children learn mathematics. Queensland, Australia: John Wiley & Sons Australia, Ltd. 

Week One - Addition

Synthesise the big ideas
In week one the following big ideas were covered:
- The four language models for mathematics are a framework that can be used to underpin
   mathematics learning. These four language models can be seen below:
   1. Student language - the language used in this level is at the students level and reflects the real
       world. An example is three birds put with four birds makes seven birds altogether (Jamieson-
       Proctor, 2016, p. 10).
   2. Materials language - the language used in this level is still at the students level but replaces
       the language used in their world with materials language, for example counters (Jamieson-
       Proctor, 2016, p. 11).
   3. Mathematics language - the language used in this level uses proper mathematics, such as add,
       subtract, equals, but does not used the symbols yet (Jamieson-Proctor, 2016, p. 12).
   4. Symbolic language - this is the final language level and involves students using the
       mathematics symbols, for example 3 + 4 = 7 (Jamieson-Proctor, 2016, p. 13).
- The language model for mathematics, which can be seen below (figure 1.1). This language model
   is a way to break down the four stages of mathematics language. On the right hand side is where
   the four stages go (see figure 1.2), and on the left hand side is where the different materials for
   each stage belong (see figure 1.3). This is a very useful diagram in breaking down the four    
   language model for mathematics, which is crucial in teaching mathematics to people of any ages.

Figure 1.1: Jamieson-Proctor, R. (2016). EDMA202/262 Mathematics Learning and Teaching 1: Week 1 Part 1. Brisbane, Australia: Australian Catholic University. 

Figure 1.2: Jamieson-Proctor, R. (2016). EDMA202/262 Mathematics Learning and Teaching 1: Week 1 Part 1. Brisbane, Australia: Australian Catholic University.

Figure 1.3: Jamieson-Proctor, R. (2016). EDMA202/262 Mathematics Learning and Teaching 1: Week 1 Part 1. Brisbane, Australia: Australian Catholic University. 

- Three strategies for addition:
   1. Count On - this is a strategy that can be used for 0, 1, 2 and 3. The child would start at the
       larger number and then count on to the final answer (Reys, Lindquist, Lambdin, Smith,
       Rogers, Falle, Frid & Bennett, 2012).
   2. Use Doubles - doubles are a basic concept which children can learn quickly (Reys et al., 2012)
   3. Use Tens - in the early years children learn how to make combinations of ten, often described
       as 'rainbow facts', and this can then be used as a strategy for addition (Reys et al., 2012).

These big ideas have changed my understanding on the weekly topic in two ways;
1. Due to the four language models of mathematics I now have a greater understanding of how to
    teach mathematics to students of any age.
2. I also have a greater understanding of addition and effective strategies that can be used to teach
    children.

Demonstrate your understanding of addition and related skills and strategies children need to assimilate and be able to use
- The concept this week was addition, addition is the joining of two or more numbers to find a total
  (Jamieson-Proctor, 2016).
- The concept of addition is applied using the skill of addition algorithm. An example of an addition
   algothrim being used can be seen in figure 1.4.
- There are three strategies that can be used for addition; count on, use double and use tens. This
   strategy has been explained in section one of this post.

Figure 1.4: Jamieson-Proctor, R. (2016). EDMA202/262 Mathematics Learning and Teaching 1: Week 1 Part 1. Brisbane, Australia: Australian Catholic University. 

Language model for addition

Figure 1.5: Language Model for Addition

Describe/demonstrate a specific teaching strategy and appropriate resource/s that could be used to assist children to understand the concept of addition
- A specific teaching strategy that could be used for children to understand the concept of addition
  is the count on strategy. "In counting on, the child gives correct number names as counting
  proceeds and can start at any number and begin counting" (Reys et al., 2012, p. 152). Children  
  would be taught to start at the highest number given and then count on.
- An example of using the count on strategy would be "Sally has 6 biscuits and was given 3 more
  by her mother." 6, 7, 8, 9.
- When practising addition in the children and materials language stage I would use resources, such
   as pictures, counters, toys, MAB blocks and other concrete materials. By using these concrete
   materials students are able to physically count on to reach their final answer. An example of how
   this would work can be seen in the Matholia Channel video.
Describe/demonstrate a specific misconception children might have in relation to addition. How would you avoid or remediate this misconception?
- A common misconception that children might have in relation to addition is that the '+' sign means
  'and' not 'plus' or 'add' (Harris, 2000). One way that this misconception can be avoided is to make
   sure that when writing for the students the '+' sign is never used as short-hand for 'and', as this
   may confuse matters for children. A way to remediate this misconception would be to make sure
   that when practising addition with students to use the correct terminology 'plus' and 'add', and to
   make a point that students know the reason behind this use of terminology.

Provide appropriate URL links to the ACARA year, strand, sub-strand, content description, elaborations and Scootle resources for the earliest mention of addition
- Addition can be first seen in the foundation year, number and algebra strand and the number and
  place value sub-strand.
- The content description for ACMNA004 is "represent practical situations to model addition and
  sharing" (ACARA, 2016)
- The elaborations are "using a range of practical strategies for adding small groups of numbers,
   such as visual displays or concrete materials" and "using Aboriginal and Torres Strait Islander
   methods of adding, including spatial patterns and reasoning" (ACARA, 2016).
- Scootle resources for addition

Provide appropriate links to resources and ideas you have sourced personally to assist students to develop concepts, skills and/or strategies related to addition
- Resources for students to understand the concept of addition
  * Addition Song
  * Concept of Addition
- Resources for students to understand the skill of addition
  *Addition Algorithm
- Resources for students to understand the strategies for addition
  * Counting On
  * Use Doubles
  * Use Tens

Provide a concise synthesis of the textbook chapter/s related to the weekly topic
- Reys et al. (2012) described six different thinking strategies for addition:
  * Commutativity is the task of learning that by changing the order of the addends. this does not
      affect the outcome of the sum, i.e. 5 + 6 = 11, 6 + 5 = 11.
  * Adding 1 and 2, i.e. 5 + 1 = 6, 6 + 1 = 7.
  * Adding doubles and near doubles, i.e. adding doubles 4 + 4 = 8. i.e. adding near doubles 7 + 8 =
     15, because 7 + 7 = 14, plus 1 is 15.
  * Counting on, i.e. 2 +6 = 8. Start at 6 then count on i.e. 6, 7, 8
  * Combinations to 10, i.e. 4 + 6 = 10, 3 + 7 = 10.
  * Adding to 10 and beyond, i.e. 8 + 5 = 13, 8 +2 = 10, plus 3 is 13.
- A goal for basic addition is a goal for the early years (Reys et al., 2012).
- Reys et al. (2012) described three different skills for addition:
  * Standard addition algorithm,
     i.e.   27
           +35
          -------
             62
  * Partial-sum addition algorithm,
     i.e.  437
          + 25
          --------    
             12
             50
           400
          --------
           462
  * Higher-decade algorithm,
     i.e. 9 + 5 = 14, the sum will have a 4 in the ones place and the tens place will always have 1 ten

References

Australian Curriculum and Assessment, Reporting Authority [ACARA]. (2016). Mathematics. Retrieved from http://www.australiancurriculum.edu.au/mathematics/curriculum/f-10?layout=1

Boney4th. (2012). Doubles and near doubles. Retrieved from https://www.youtube.com/watch?v=7PRIBdFtRNA 

Boney4th. (2012). Make 10 addition strategy. Retrieved from https://www.youtube.com/watch?v=E4Kq28ayZiU

Education Services Australia. (2016). Scootle: Mathematics. Retrieved from http://www.scootle.edu.au/ec/search?accContentId=ACMNA004&userlevel=(0)#backToTop 

Harris, A. (2000). Addition and subtraction. Retrieved from http://ictedusrv.cumbria.ac.uk/maths/pgdl/unit5/A&S.pdf 

Harry Kindergarten Music. (2014). When you add with a pirate. Retrieved from https://www.youtube.com/watch?v=WT_wvvEvkw4

Jamieson-Proctor, R. (2016). EDMA202/262 Mathematics learning and teaching 1: Week 1 part 1. Brisbane, Australia: Australian Catholic University. 

Matholia Channel. (2013). Addition by Counting On. Retrieved from https://www.youtube.com/watch?v=PUY072JHE4g 

Professor Pete's Classroom. (2014). Teaching the addition algorithm with regrouping. Retrieved from https://www.youtube.com/watch?v=F9mnIXEbTNI 

Reys, R., Lindquist, M., Lambdin, D., Smith, N., Rogers, A., Falle, J., Frid, S., & Bennett, S. (2012). Helping children learn mathematics. Queensland, Australia: John Wiley & Sons Australia, Ltd. 

Walkin, K. (2013). Teaching concept of addition. Retrieved from https://www.youtube.com/watch?v=JZh298VpdhY